圆钢管柱-H形梁子结构抗连续性倒塌性能试验

简述：

       以H形梁-圆管柱外环板焊接节点为研究对象，对节点及其连接的梁柱构件组成的子结构施加竖向单调荷载，直至试件在大变形条件下完全丧失竖向承载力。梁外端设置固定铰约束以发挥水平拉结力，中柱底端设置竖向滑动约束以模拟中柱失效工况。

试验方案：

（1）试件设计

试件采用Q345B钢材。梁截面为H300×150×6×8mm，圆管柱截面为Ø351×12mm，外环板厚度为8mm，最小外伸宽度为25mm，节点区环板外伸段与梁端采用全焊连接。试件命名为CO-W。试件水平长度为4500mm，梁跨高比为15。试件节点区构造如图1所示。

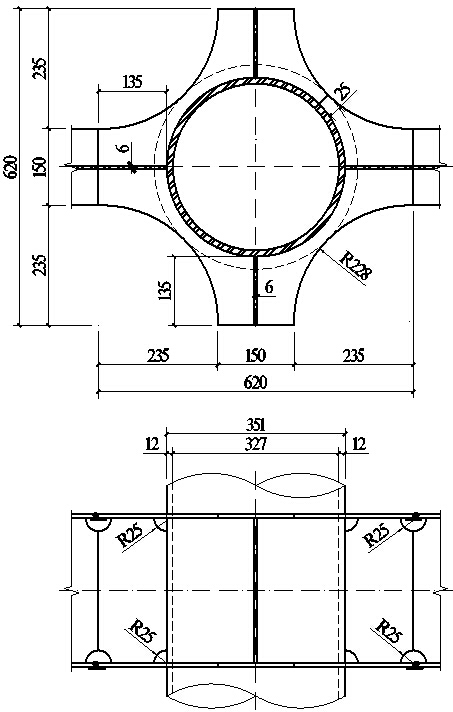
图1  试件CO-W节点区构造（尺寸单位：mm）

（2）  钢材材性

    钢材的材性由标准拉伸试验确定，材性试验的试样与试验构件为同批钢材。每种批次及厚度的钢材各取三个试样。试件CO-W的材性试件分为3组：

（1）BF-8，取自梁翼缘，名义厚度为8mm；

（2）BW-6，取自梁腹板，名义厚度为6mm；

（3）CT-12，取自圆管柱，名义厚度为12mm。

  三组组材性试验的工程应力（σEng）-工程应变（εEng）关系曲线见图2，变换为真实应力-应变结果后的平均值数据列于表1。

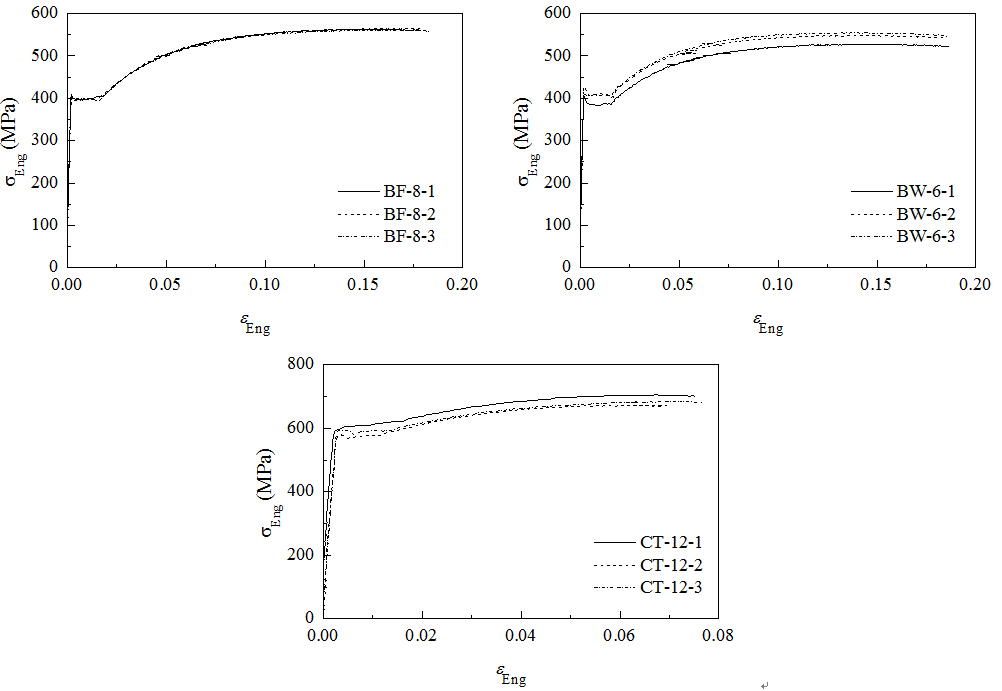
图2  试件CO-W钢材材性试验的工程应力-应变关系曲线

表1 试件CO-W的钢材材性试验结果

试件编号	屈服强度fy(MPa)	抗拉强度fu(MPa)	强屈比fu/fy	断面收缩率	断后伸长率
BF-8	401	668	1.67	0.62	0.31
BW-6	407	638	1.57	0.67	0.31
CT-12	588	736	1.25	0.68	0.22

（3）  加载方案

（3.1）试验装置如图3所示，由端部的三角反力架、底部的可拆卸地梁以及中部的柱底滑动约束装置组成。

    （1）整套装置为对称的水平自平衡反力装置，可自行平衡由试件在发挥悬链线效应时对梁端支座产生的较大水平力。三角反力架通过耳板及销轴与梁端相连，实现平面铰约束。

    （2）试件柱顶连接作动器加载头，加载头仅施加竖向荷载。

    （3）柱底滑动约束装置使中柱仅进行竖向滑动，中柱底部有约400mm竖向滑动空间。

（3.2）加载制度采用位移控制的单调加载方式，分级加载并观测现象。对梁柱子结构试件的中柱柱顶施加竖向荷载的方式，加载速率不大于7mm/min，满足静力加载要求。　

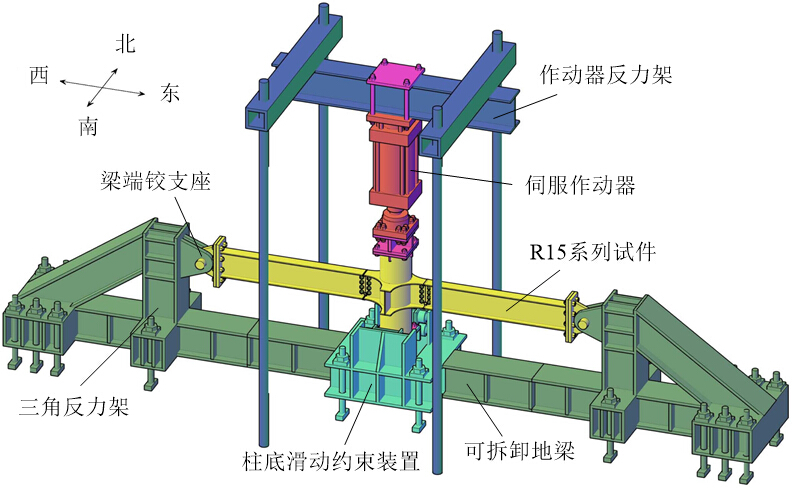
图3 加载装置

（4） 测试方案

    本试验测量目标包括：

    （1）柱顶荷载：由作动器力传感器获取；

    （2）节点试件的竖向构形：由位移计获取；

    （3）梁柱重要截面的应变分布及内力状态：由应变片获取；

    （4）支座位移监测，由位移计获取。

位移计的测点布置如图4所示。应变片测点布置如图5所示，其中截面W2/E2上下翼缘轴向应变采用大量程应变计（最大应变量程可达0.15）。

图4 试件CO-W的位移计测点布置图

图5 试件CO-W的应变片测点布置图

（5） 分析参数

     （5.1）将柱顶竖向位移Δ采用单侧梁的轴线间长度Lb=2250mm进行归一化，定义为梁弦转角θ，用以表征梁柱子结构的相对变形量。

     （5.2）截面承载力

               根据表1的钢材材性试验结果，取梁截面钢材的实测屈服强度为fy=400MPa，计算得：

               梁截面全截面轴拉屈服承载力  Np =1641 kN

               梁截面全截面塑性抗弯承载力  Mp =188 kNm

               梁截面腹板抗剪屈服承载力     Vp =394 kN

    （5.3）截面承载力

如图6所示，在最不利截面W2/E2达到其理论全截面塑性抗弯承载力，即形成塑性铰时，梁柱子结构的竖向承载力Fp =194kN。

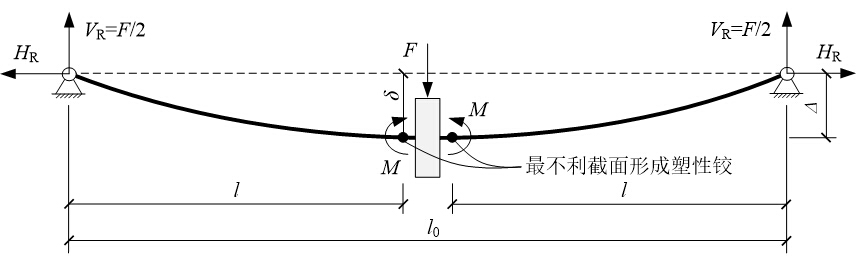
图6 梁柱子结构的的简支梁计算模型

（5.4）截面内力

       位于铰支座附近的梁截面W1/E1在加载过程中保持弹性，因此截面轴力N1、弯矩M1以及剪力V1，可分别依据下式进行计算，式中E=2.06×105MPa为钢材弹性模量，A为截面面积，I为截面绕强轴惯性矩，(Σε)/n为参与计算的n个应变的平均值，Δε/Δh为截面曲率，l1为计算截面距反弯点（即梁端铰支座）的长度。

如图7所示，根据力的平衡原理可采用下式计算截面W1/E1相邻铰支座的竖向反力VR和水平反力HR：                                                                             如图7所示，若已知梁段上任意截面竖向位移δi及其与铰支座的水平距离li，可依据下式计算任意截面内力：

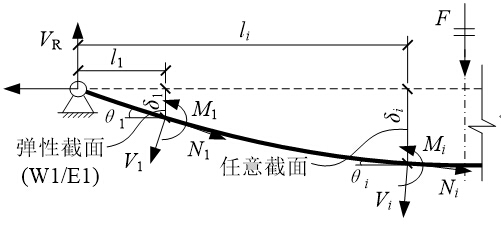
图7 试件支座反力与截面内力分析模型

试验现象：

试验观察和破坏现象

试验加载的最大位移为Δmax=361mm，对应于梁弦转角为θmax=0.161rad，试验结束时节点已完全失效。试验后的节点部位破坏形态如图8所示，试件的整体变形如图9所示。试件的破坏发生在节点外伸段与梁端的连接部位，破坏现象及破坏过程列于表2中，表中参数Fp与θ的含义已在“分析参数”一节中说明。

图8 试件CO-W的节点部位破坏形态

图9  试件CO-W的整体变形

表2 试件CO-W的破坏现象及破坏过程

西侧	东侧
梁W2截面附近上翼缘屈曲	梁E2截面附近上翼缘屈曲（A）
梁W2截面下翼缘断裂，裂纹扩展至腹板 （C，θ=0.108rad，F=1.36Fp）	梁E2截面下翼缘断裂，裂纹扩展至腹板 （B，θ=0.094 rad，F=1.35Fp）
梁W2截面裂纹开展接近腹板上边缘 （E）	梁E2截面上翼缘断裂，东侧梁与中柱脱开 （D，θ=0.160 rad，F=0.33Fp）

试验数据：

  主要数据——循环加载试验曲线 　

 （1）试件竖向变形形态发展

    图10为加载过程中，试件的整体竖向变形图，其中Δ为柱顶加载位移，位移计测点的位移值δ以向下为负。

   

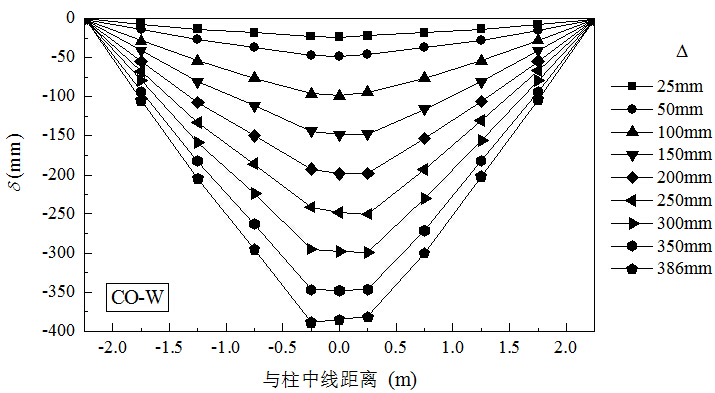
图10  试件CO-W的竖向变形形态发展

（2）荷载-位移曲线

试件CO-W的柱顶荷载-柱顶位移关系曲线如图11所示，标明了各关键试验现象，并分别对应表2中各图。

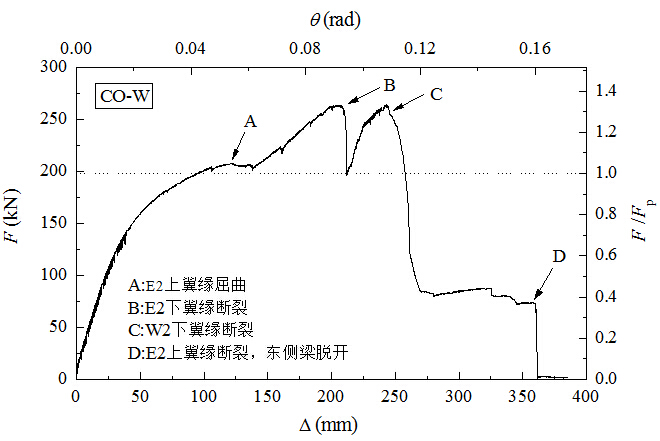
图11 试件CO-WB的柱顶荷载(F)-柱顶位移(Δ)关系曲线

（3） 弹性梁段截面W1/E1应变发展曲线

         图12为梁截面W1/E1所布置的应变测点的发展曲线。

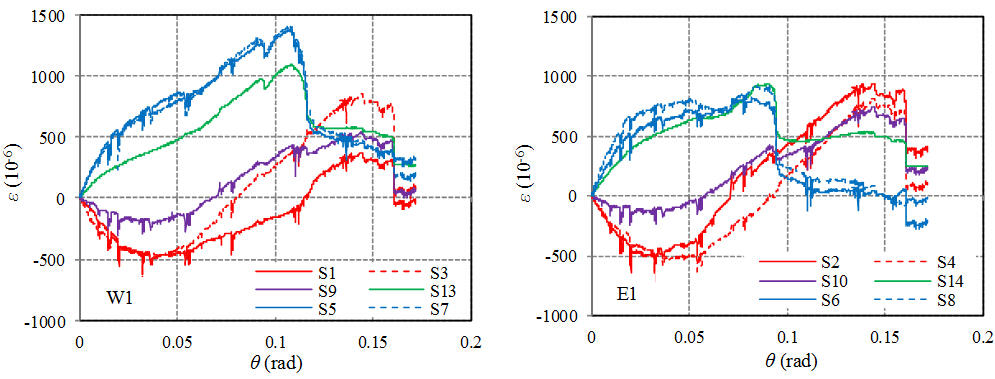
图 12  试件CO-W的W1/E1截面各测点的应变发展曲线

（4） 最不利截面W2/E2的应变发展曲线

         图13为最不利截面W2/E2的上下翼缘轴向应变测点的应变发展曲线，图13中T表示测点位于梁截面的上翼缘，B表示测点位于梁截面的下翼缘。

    

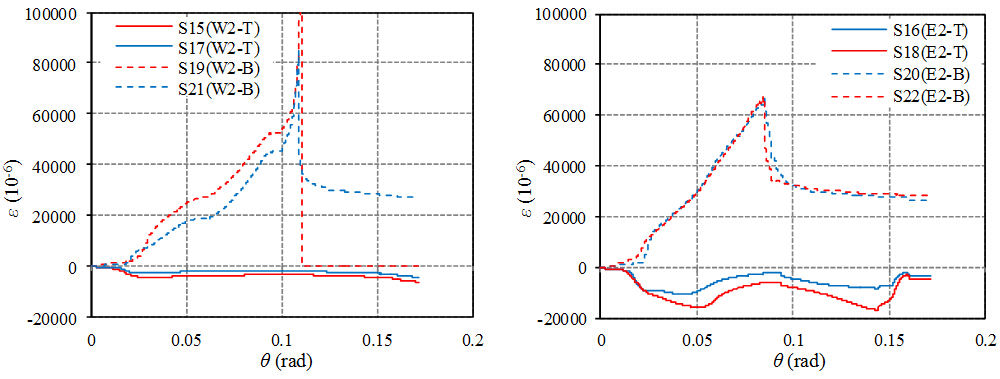
图13  试件CO-W 的最不利截面W2/E2的上下翼缘测点的应变发展曲线

（5）内力与支座反力发展曲线

        图14为梁截面W1/E1的轴力N和剪力V的发展曲线，图15为西侧梁和东侧梁各测试截面的弯矩M的发展曲线。截面内力的计算方法已在“分析参数”一节中说明。图14和图15中纵坐标对    轴力N、剪力V以及弯矩M分别采用Np，Vp和Mp进行归一化。

       对母材、熔敷金属和热影响区三种材料制成的圆周平滑槽口试件进行单轴拉伸试验，得到的各试件力-变形（标距段）试验曲线如图11所示。

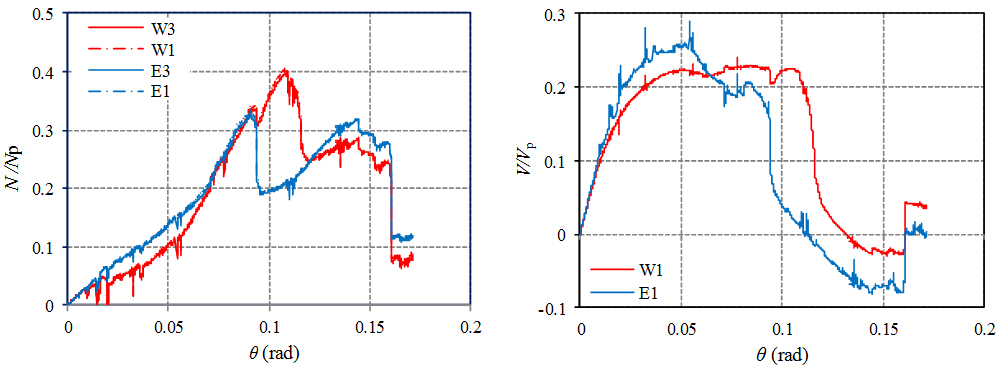
图 14  试件CO-W的W1与E1截面轴力和剪力发展曲线

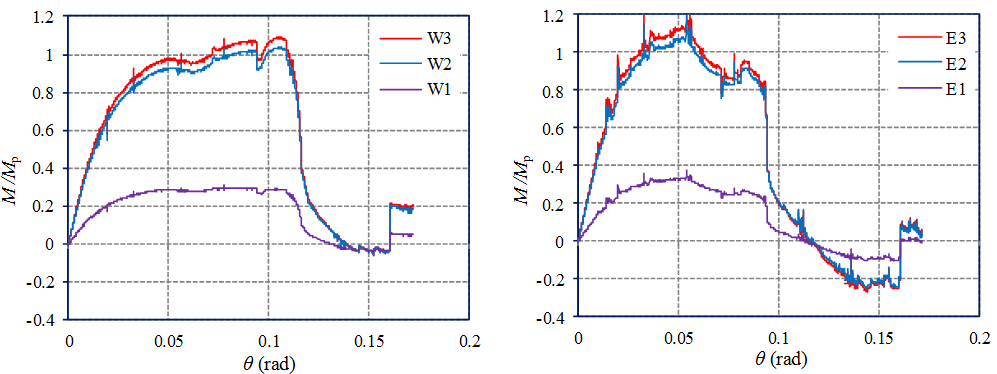
图 15  试件CO-W的截面弯矩发展曲线

参考文献：

关联文献及联系作者 　　

以下文献公布了此项试验的部分关联数据。(The papers/literatures following have published the relating data of this research.)

李玲, 王伟, 陈以一. (2015). 钢管柱框架节点在连续性倒塌工况下的破坏模式与鲁棒性. 建筑结构学报,36(4):9-15.　

王伟, 李玲, 陈以一，严鹏. (2014). 圆钢管柱-H形梁外环板式节点抗连续性倒塌性能试验研究. 建筑结构学报, 35(7):26-33.

Ling LI, Wei WANG, Yiyi CHEN, Yong LU. (2013). Experimental investigation of beam-to-tubular column moment connections under column removal scenario. Journal of Constructional Steel Research, 88:244-255.

联系作者：

王伟（Wei Wang）

Tel.: +86-21-6598 2926; fax: +86-21-6598 4976；weiwang@tongji.edu.cn

支持单位：

国家自然科学基金项目（51008220）

土木工程防灾国家重点实验室基金项目 （SLDRCE09-B-02）